很多语言都有Hash Table这种数据结构,有的叫哈希表,有的叫散列表,有的叫字典,有的叫map。大体上讲,这就是一种存储键值对的数据结构,通过hash算法,将给定的key算出一个hash值,将value存到hash值对应的地方。下次查找key的时候,以同样的hash算法算出key的hash值,到相应的地方找到该value。从原理可以看出,这种数据结构的好处是,无论多大的一个数据量,算法复杂度总是Ο(1)的。所以大多数的编程语言都实现了这种数据结构。
1.什么是hash碰撞?
那么从上面介绍的原理中可以看出,这种数据结构的关键就是hash算法。hash算法决定了你的key将在什么地方保存value,如果你要让各种对象都可以作为key的话,你就要为它们实现hash算法。hash算法又是一个很神奇的算法。
一个设计良好的 hash 算法,具有以下特性:
- 压缩性:任意长度的数据都可以通过hash来压缩(或扩展)到相同长度
- 抗计算原性:给定一个hash结果h,寻找原来的M来满足H(M)=h是计算困难的。(hash是一种单向的函数,这个功能很强大。例如,我们在数据库保存用户的密码并不是保存密码明文,而是保存密码明文的hash值,验证密码是否正确的时候将明文hash之后与数据库保存的hash值对比即可。这样即使数据库泄露,也不会泄露用户的密码)
- 抗碰撞性。找到两个明文M,M’ 使hash值 H(M)=H(M’)是计算困难的
正因为有第三点,所以我们的hash表才能正常工作。但实际上,由于hash将任意长度生成固定长度的值,所以必然可能存在两个不同的值M和M’,它们的hash值相等,数据结构必须能正确处理这种情况。本文就来讨论这种情况的一些解决方案——如何处理hash碰撞(Hash Collision)。在开始讨论解决方法之前,我们先要明确下面几点:
- 字典(hash表等称呼在本文就统称为“字典”了)必须能够处理无限大的数据量
- 字典要尽量保持Ο(1)的查询速度
- 字典要能够处理hash一致,但是值不一致的情况,屏蔽底层细节提供保存、查询等功能
- hash函数的散列度越高越好(减少hash碰撞的情况)
2.字典的工作原理
在《为什么list不能作为字典的key?》一文中详细介绍了字典的工作原理。
字典其实是用一个array来保存key-value pair的,value保存的位置就是hash key的值。保存的时候计算hash(key)拿到下标,将value保存到该位置,查找的时候计算hash(key)得到下标,到该位置拿到value。这样就可以做到Ο(1)的速度。
需要注意的是,因为“hash碰撞”的存在,hash(key)得到的下标的位置存放的元素并不一样是我们要找的元素。所以一个准确的查询过程应该是:
hash(key)拿到下标- 拿到下标的元素(实际上Array并不只存放的value,而是一个key-value键值对),比较如果该地址的key==我要找的key,那么这个value才是我要找的value
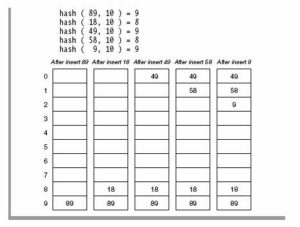
举个例子,将 {89, 18, 49, 58, 9} 存入hash表中。
存放的步骤如下:
- 计算89的hash位置(为什么是
hash(key, size),因为我们得到的下标值必须是一个array容量内的下标,所以跟size mask一下),得到9,位置9空,放进这个位置 - 计算18的位置并存放,同上
- 计算49的位置,发现这个位置已经有元素了:
- 如果这个元素==89,说明我们想要存放的元素已经放好了,结束
- 如果!=89,说明此位置发生hash碰撞,我们将49存入下位置9的下一个位置——位置0
- 继续存放下一个元素,如果没发生hash碰撞就执行步骤1,如果发生hash碰撞就执行步骤3
查询的时候,比如要查询49:
- 计算
hash(49)的值,得到下标9,发现下标9的元素key不等于49 - 去位置1,发现key等于49,找到,结束
3.Probing
上面觉得这个例子,其实就是解决hash碰撞的一种方案,叫做“Probing”(其实是最简单的一种Probing,叫做Liner Probing)。如果发生了hash碰撞,就使用一种策略在Array中找到一个空的位置。查找的时候只要使用同样的策略去找,肯定能找回这个元素。Probing有几个很关键的问题需要注意:
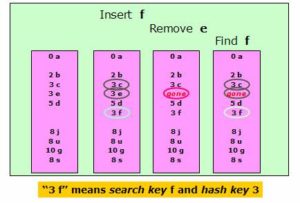
3.1惰性删除
回想上面这个例子,现在我们要从字典中删除89这个元素,如果直接将89设置为空的话,就会产生很严重的问题:如果此时存放49,计算hash得9,位置9为空,放入,就会出现两个49在字典中;如果此时查找49,发现位置9为空,得到结果49不存在;等等。
所以要删除元素的时候,我们并不会真的将这个位置的元素删除,位置设置一个特殊的flag,表示这个地方的元素已经被删除了。并不会影响49这个元素的查询(在本例子中)。
这种方案存在的问题是:如果字典要经常删除元素,就会留下大量“尸体”,而存放新的元素需要不断扩大字典。但是如今存储空间非常廉价,所以这个方案依然是比较有效的。
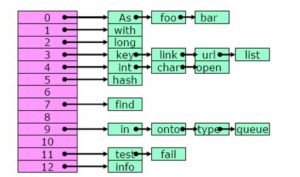
3.2聚集问题
在文章一开始我就提到,字典的散列度越高越好。试想如果我们计算10个元素的hash值都一样,那么每次存放和读取都会发生Probing,读取时间就会变成最高Ο(n)复杂度。
一个简单的策略是,当字典中存放的元素超过70%,就扩大字典体积。下图描述了一个散列度尚可的字典,有一小部分的聚集,当保存的元素超过70%就扩张。
这个问题其实很有意思,有一种web攻击叫做“Hash碰撞攻击”,简单而致命。一般的web服务器都用字典这种简单有效的数据结构来保存请求参数,如果我们发送一个请求,里面所有key都是相同的hash(所以如果想要使用这种攻击方式,必须知道目标服务器/编程语言的hash策略),服务器去保存你的参数时耗费的时间从Ο(1)变成Ο(n).这里有个例子,展示了PHP保存正常的65535个int值只需要0.021s,如果保存一个恶意构造的65535个int,需要42s!
4.其他Probing方式
所以,hash函数必须减少碰撞的机会。除此之外,probing也要减少计算的机会,也就是说,probing的策略也要尽量提高散列度。
4.1 Quadratic Probing
顾名思义,就是通过一个二次方程计算下一个位置。举个例子,上面的字典我们使用如下策略,如果当前位置冲突,就使用当前位置 + 2^n来保存,即K+1,K+4,K+9,结果如下。
明显比Liner Probing的散列度高了很多。
Python使用的方程是:
|
1 2 3 |
j = (5*j) + 1 + perturb; # perturb = j = hash(key) perturb >>= PERTURB_SHIFT; use j % 2**i as the next table index; |
如果j=3,size=32的时候,序列如下:
3 -> 11 -> 19 -> 29 -> 5 -> 6 -> 16 -> 31 -> 28 -> 13 -> 2…
这里加了个perturb,很有意思,通过这里的伪代码我发现这个值也是通过hash计算出来的。这就意味着,对Python的字典进行hash碰撞攻击是非常困难的。
4.2 Double Hashing
发生冲突的时候,使用另一个hash函数计算probing的位置。
4.3 总结
这里有一个权衡,就是存取效率(每次计算耗费的时间)和散列度的权衡(计算的次数)。
如果存取效率高了,也就是计算probing的速度快了,那么散列度就会下降。Liner Probing是一个极端,存取效率很高,只要+1就可以,但是probing的次数很多。
散列度如果高了,比如Double Hashing,使用hash函数来probing肯定散列度很高,但是每次计算都要使用hash函数,计算效率就下降。
二次方程probing是一个权衡的策略,用的比较多(Python)。
5. Closed Hashing
上面提到probing的这种方法,本质上都是“当位置冲突了想办法找到另一个位置”,存放的结构是一维数组。都叫做“Open Adressing”。
还有一种“Open hashing”,也叫做“Separate Chaining”。将相同hash值的元素用Linked List链接在一起,如果Hash碰撞,在链表中找key相等的那个元素。这种形式省去了计算地址的时间,相当于Liner Probing更极端的一种形式,存取非常块,但是聚合问题最大。实现也更加复杂,需要编程语言动态分配内存。
参考资料:
- How can Python dict have multiple keys with same hash? 这里有些回答非常精彩,基本解释了散列值工作的详细过程
- Hash碰撞与拒绝服务攻击 这篇文章讲了hash算法以及碰撞攻击
- Python dictionary implementation Laurent写了很多Python实现讲解,我从他博客学到了很多东西
- Collision Resolution CMU讲义,大多数讨论hash碰撞的地方都引用了此文,非常易读
- wiki open addressing
- hash碰撞攻击
- Meaning of Open hashing and Closed hashing


Pingback: Java:HashMap原理与设计缘由 – Python量化投资
Pingback: 有关 TLS/SSL 证书的一切 | 卡瓦邦噶!